网络流是图论中的一个重要的问题,关于其介绍可以参考OI-Wiki中的内容(下1,建议先行阅读)。本文就网络流中最大流问题介绍几种算法。
最大流
给出一个源点$S$以及汇点$T$,求$S\to T$的最大流量。
剩余容量
对于一条边$<u,v>$,定义其容量为$c(u,v)$,其流量为$f(u,v)$,那么我么可以得到它的 剩余容量为$c_{f}(u,v)=c(u,v)-f(u,v)$,即容量与流量的差(也就是还能承载多少流量)。值得注意的是,由流函数定义中的$f(u,v)=-f(v,u)$,我们可以发现$c_{f} (v,u)=c(v,u)-f(v,u)=c(u,v)+f(u,v)=f(u,v)$(反向边没有容量),这就是 虚边(反向边)的剩余容量。可以发现$c(u,v)=c_f(u,v)+c_f(v,u)$,即对于一条边而言,其容量为实边与虚边流量和。
残差网络
由上述残差容量引入,对于网络中所有节点以及剩余容量大于0的边构成的子图,我们称为 残差网络(包含虚边)。
增广路
很显然,在原图$G$中如果存在一条路径上所有的边剩余容量都大于0,则这条路被称为增广路(还能承载更多流量)。实际上,寻找增广路就是在残差网络中寻找一条从源点$S$到汇点$T$的简单路径。
EK(Edmond-Karp)算法
由我们刚刚引出的一些概念,我们可以想到一种非常直观的求最大流的方法——寻找增广路,找到最小流量并对其增广。
更具体地说,就是BFS遍历整个残差网络,记录路径,当遇到汇点时即对路径边进行增广,增广的值自然就是最小的剩余容量,同时对答案也增加这个值,从源点重复多次此操作,直到找不到增广路。
为什么需要反向边?下面这张图可以很好地解释:
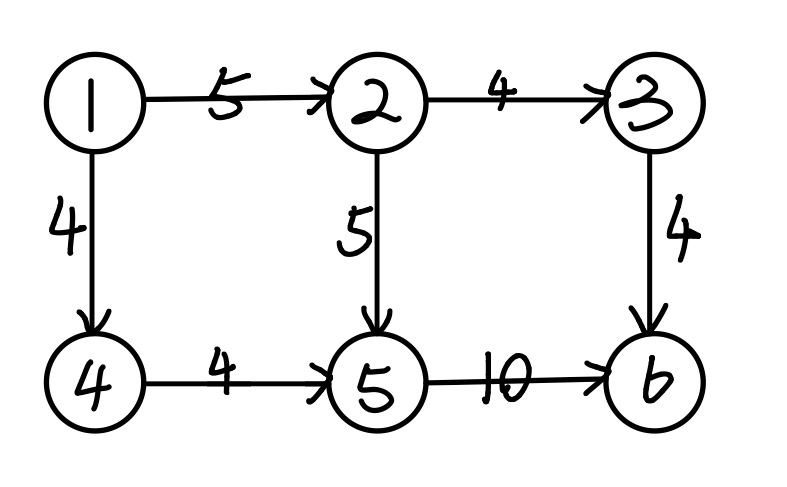
反向边实际上是给算法一个“后悔”的机会。例如,如果第一次进行增广的时候选择的是路径$ 1\to2\to5\to6$,路径最大流量为5,无法再进行增广,这与实际最大流9不符。这时候,我们引入反向边$<5,2>$,其残差流量为5,算法就能够再一次进行增广,路径为$ 1\to4\to5\to2\to3\to6$,路径最大流量为4,累计最大流为9,正是我们需要的答案。
算法时间复杂度$O(|V||E|^2)$。
Dinic算法
与EK算法不同的是,在寻找到一条增广路后,它不需要从源点重新开始寻找增广路,而是可以通过DFS实现多次增广。
更具体的说,首先使用BFS对节点将节点分层,对于每一个阶段按DFS搜索顺序增广(只能走深度不断加深的路径),重复以上操作直到不存在增广路。
算法时间复杂度$O(|V|^2|E|)$,特别地,当算法用于二分图最大匹配问题的时候时间复杂度为$O(|E|\sqrt{|V|})$。
ISAP算法
与Dinic算法类似,ISAP算法优化其中BFS的次数,仅需一次BFS标记深度。
在Dinic算法中,每次DFS结束后都需要用BFS重新去维护节点层次信息,而在ISAP中,算法从汇点$T$到源点$S$只进行一次BFS将节点分层,再从$S$到$T$进行DFS,若出现当前节点流出的流量小于流入的流量时,对其进行加深,当$S$的深度大于等于$|V|$时算法终止。
算法时间复杂度$O(|V|^2|E|)$。
